Parity and Pigeons
Legend
 |
Interactive |
 |
Notice |
 |
Slideshow |
 |
Video |

| Konigsberg Interactive: Help a monster cross the bridges of Konigsberg |  |

arrow_back
arrow_forward
arrow_upward
arrow_downward

| Handshaking Monsters Interactive: None |  |

arrow_back
arrow_forward
arrow_upward
arrow_downward

| Konigsberg Tweak Interactive: Help a monster cross the bridges of Konigsberg, but now add and remove bridges! |  |

arrow_back
arrow_forward
arrow_upward
arrow_downward

| Chessboard Interactive: Lay dominoes on a chessboard with the corners removed |  |

arrow_back
arrow_forward
arrow_upward
arrow_downward

| Chessboard Interactive Tweaked: Lay dominoes on a chessboard and pick which squares to remove |  |

arrow_back
arrow_forward
arrow_upward
arrow_downward

| Monsters with Umbrellas Interactive: Find a loop in a tangle of ropes |  |
Under construction....

arrow_back
arrow_forward
arrow_upward
arrow_downward

| Loopy Monsters Interactive: Keep track of ropes under umbrellas while finding loops |  |
Under construction....

arrow_back
arrow_forward
arrow_upward
arrow_downward

| Monsters with Sox Interactive: How many sox do you need for a pair? |  |

arrow_back
arrow_forward
arrow_upward
arrow_downward

| Pigeonhole Interactive: Help the pigeons find a pigeonhole |  |

arrow_back
arrow_forward
arrow_upward
arrow_downward

| A shortcut for those who need it: Take the sidetrack to avoid the most intricate part of this Exploration. If you're feeling lost, by all means use this, but you will miss a truly beautiful piece of mathematics |  |
A shortcut for those who need it: Take the sidetrack to avoid the most intricate part of this Exploration. If you're feeling lost, by all means use this, but you will miss a truly beautiful piece of mathematics

arrow_back
arrow_forward
arrow_upward
arrow_downward

| Messy Monsters: Some Monsters offer insight |  |

| Konigsberg Intro: Introduces the Bridges of Konigsberg problem. |  |

arrow_back
arrow_forward
arrow_upward
arrow_downward

| Pigeons Explained: Describes what's going on when too many pigeons try to fit into a small pigeon roost. Otherwise known in mathematics as the Pigeonhole Principle. |  |

arrow_back
arrow_forward
arrow_upward
arrow_downward

| Handshaking Monsters Explained: Explains what's happening when a bunch of monsters start shaking hands and what that has to do with pigeons. |  |

arrow_back
arrow_forward
arrow_upward
arrow_downward

| Konigsberg Tweak: Exploring changes to the Bridges of Konigsberg problem. |  |

arrow_back
arrow_forward
arrow_upward
arrow_downward

| Try Some Monsters: Where to find insight into the Bridges of Konigsberg problem? |  |

arrow_back
arrow_forward
arrow_upward
arrow_downward

| Monsters In Konigsberg & Domino Intro: Monsters take to the streets of Konigsberg to help solve the famous problem. Then, a new problem is introduced, involving a chessboard and dominoes. |  |

arrow_back
arrow_forward
arrow_upward
arrow_downward

| Domino Tweak: How we might tweak our Chessboard Interactive. |  |

arrow_back
arrow_forward
arrow_upward
arrow_downward

| Dominoes Explained: Explains the insights you might have observed in the last Interactive. |  |

arrow_back
arrow_forward
arrow_upward
arrow_downward

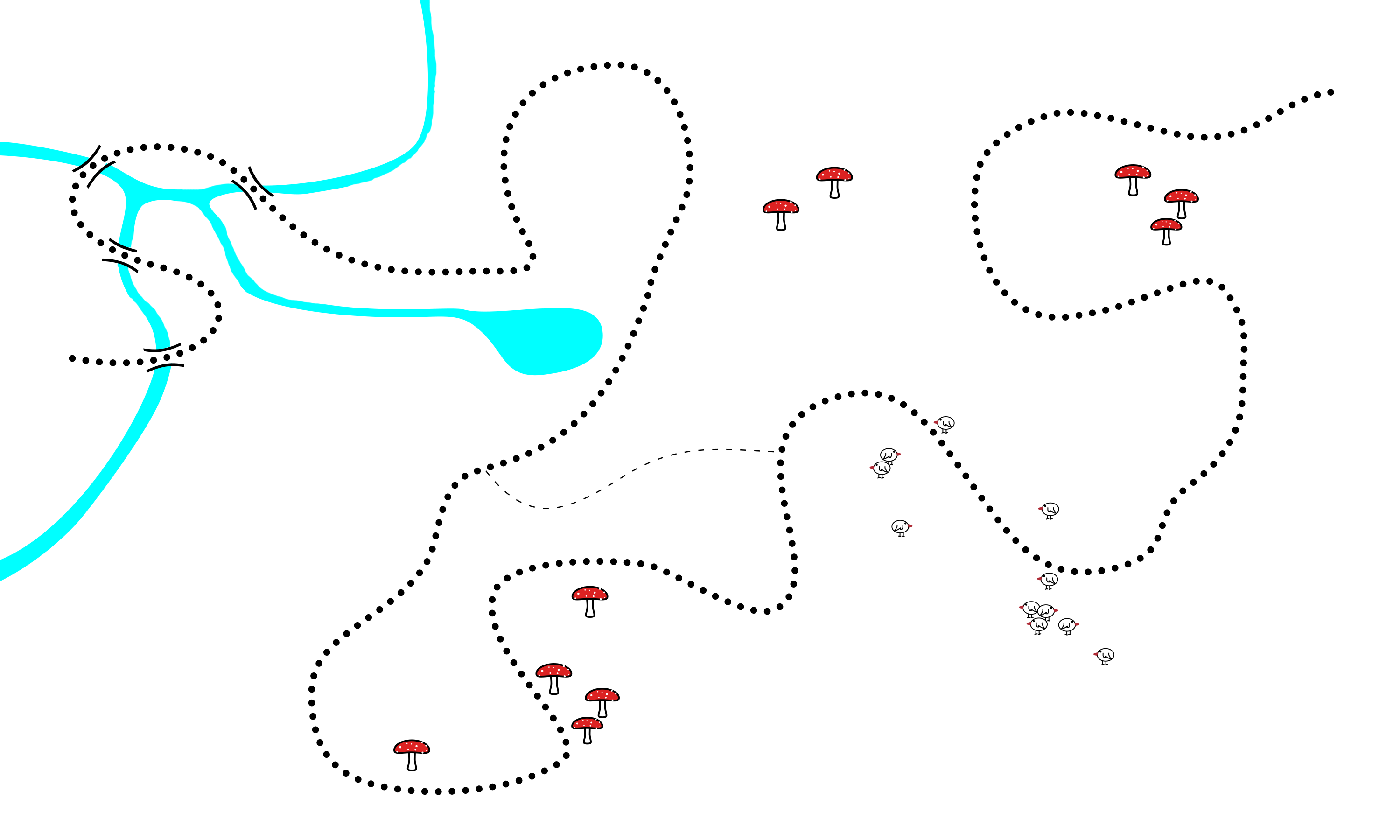
| Konigsberg Graph: Describes how the Bridges of Konigsberg and Messy Monsters with Umbrellas are really both different views of the same mathematical object called a graph. |  |

arrow_back
arrow_forward
arrow_upward
arrow_downward

| Loops: Examines loops in problems related to the Bridges of Konigsberg and Messy Monsters with Umbrellas. Specifically mathematical loops in their corresponding graphs. |  |

arrow_back
arrow_forward
arrow_upward
arrow_downward

| Konigsberg Induction: The beautiful induction argument that shows when problems like the Bridges of Konigsberg and Messy Monsters with Umbrellas can be solved. A pictorial argument involving graphs. |  |

arrow_back
arrow_forward
arrow_upward
arrow_downward

| Sox Explained: A beautifully simple way of guaranteeing you can pick a pair of sox from your drawer, even if you happen to be a three-footed monster (in which case, obviously, you'll want a triple). |  |

arrow_back
arrow_forward
arrow_upward
arrow_downward

Dominoes and Chessboard:
Problems with cover partial chessboards with dominoes.
Age Range:
7+, younger audiences will need more guidance interpreting problems, but all will have fun playing with it. Great for everyone!
Mathematics:
Parity. Matching. Geometric intuition. Exploring with Trial and Error.
Click for more!
Problems with cover partial chessboards with dominoes.
Age Range:
7+, younger audiences will need more guidance interpreting problems, but all will have fun playing with it. Great for everyone!
Mathematics:
Parity. Matching. Geometric intuition. Exploring with Trial and Error.
Click for more!
Konigsberg:
Explore the famous Bridges of Konigsberg problem. Simplify and alter the problem to shed light on what is happening. Finally, clever counting reveals the solution.
Age Range:
5+, younger audiences will move slower, but everyone will get something from these activities
Mathematics:
Parity. Exploring with Trial and Error. Simplifying and altering questions as a mode of inquiry.
Click for more!
Explore the famous Bridges of Konigsberg problem. Simplify and alter the problem to shed light on what is happening. Finally, clever counting reveals the solution.
Age Range:
5+, younger audiences will move slower, but everyone will get something from these activities
Mathematics:
Parity. Exploring with Trial and Error. Simplifying and altering questions as a mode of inquiry.
Click for more!
Messy Monsters:
Using Messy Monsters to see reverse of Bridges of Konigsberg problem
Age Range:
10+, younger audiences will move slower, but the arguments are beautiful and well worth showing everyone.
Mathematics:
Induction. Exploring with Trial and Error. Elementary Graph Theory
Click for more!
Using Messy Monsters to see reverse of Bridges of Konigsberg problem
Age Range:
10+, younger audiences will move slower, but the arguments are beautiful and well worth showing everyone.
Mathematics:
Induction. Exploring with Trial and Error. Elementary Graph Theory
Click for more!
Monster Handshake:
If a group of students shake hands, must two of them have shaken the same number of hands?
Age Range:
5+, younger audiences will move slower, but everyone, including adults, will be delighted and surprised by these activities.
Mathematics:
Pigeonhole Principle. Exploring with Trial and Error. Simplifying as a mode of inquiry.
Click for more!
If a group of students shake hands, must two of them have shaken the same number of hands?
Age Range:
5+, younger audiences will move slower, but everyone, including adults, will be delighted and surprised by these activities.
Mathematics:
Pigeonhole Principle. Exploring with Trial and Error. Simplifying as a mode of inquiry.
Click for more!
Pigeonhole:
How easy is it to find a pair of sox, or fill pigeonholes with pigeons?
Age Range:
5+, younger audiences will move slower, but everyone will get something from this task.
Mathematics:
Pigeonhole Principle. Exploring with Trial and Error. Simplifying and altering questions as a mode of inquiry.
Click for more!
How easy is it to find a pair of sox, or fill pigeonholes with pigeons?
Age Range:
5+, younger audiences will move slower, but everyone will get something from this task.
Mathematics:
Pigeonhole Principle. Exploring with Trial and Error. Simplifying and altering questions as a mode of inquiry.
Click for more!